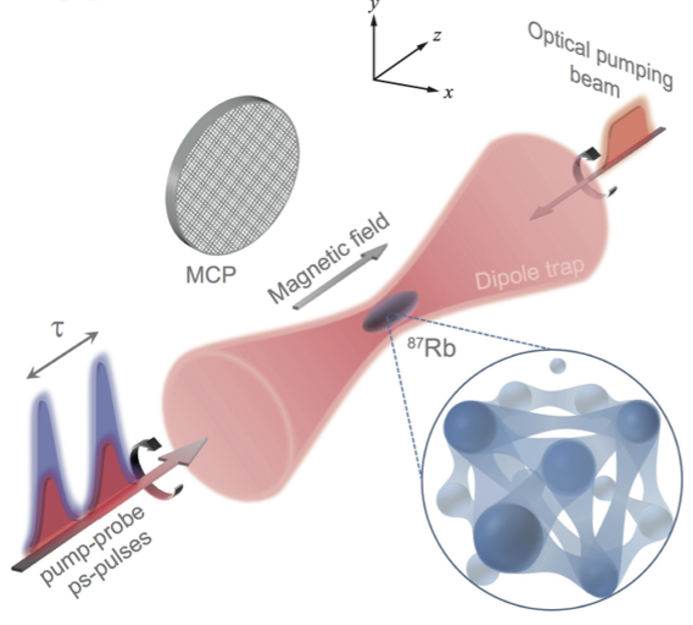
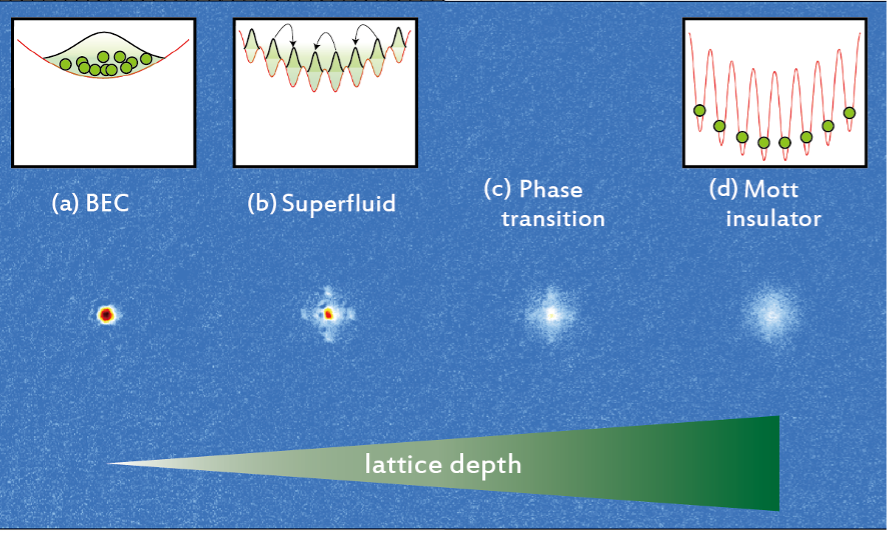
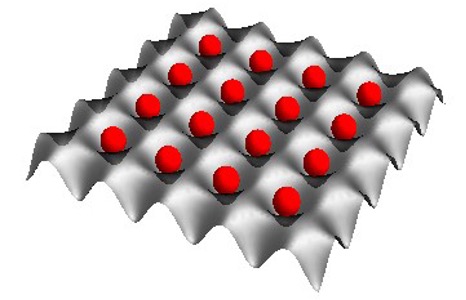
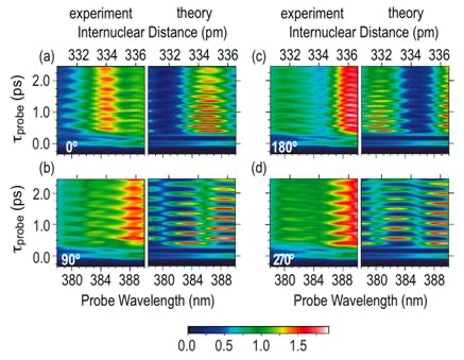
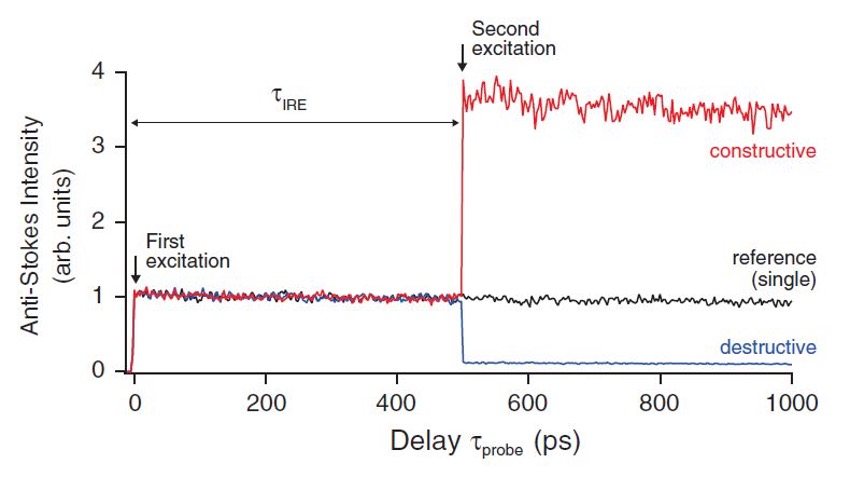
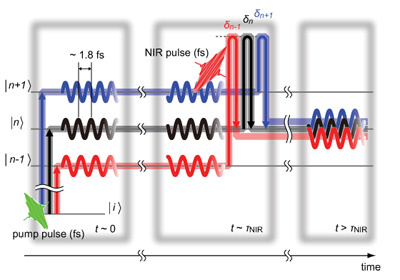
“Ultrafast energy exchange between two single Rydberg atoms on a nanosecond timescale,”
Y. ChewY. Chew, T. Tomita, T. P. Mahesh, S. Sugawa, S. de Léséleuc & K. Ohmori
Nature Photonics (2022)
|
“Ultrafast many-body dynamics in an ultracold Rydberg-excited atomic Mott insulator,”
V. Bharti, S. Sugawa, M.Mizoguchi, M. Kunimi, Y.Zhang, S. de L s leuc, T.Tomita, T. Franz, M.Weidemüller, K. Ohmori
arXiv:2201.09590 (2022).
|
“Ultrafast energy exchange between two single Rydberg atoms on the nanosecond timescale,”
Yeelai Chew, Takafumi Tomita, Tirumalasetty Panduranga Mahesh, Seiji Sugawa, Sylvain de Léséleuc, and Kenji Ohmori
arXiv:2111.12314 (2021).
|
“Engineering quantum wave-packet dispersion with a strong non-resonant femtosecond laser pulse,”
Hiroyuki Katsuki, Yukiyoshi Ohtsuki, Toru Ajiki, Haruka Goto, and Kenji Ohmori
Phys. Rev. Research. 3, 043021 (2021).
|
“Optimal control for suppressing wave packet spreading with strong non-resonant laser pulses,”
Yukiyoshi Ohtsuki, Tomotaro Namba, Hiroyuki Katsuki and Kenji Ohmori
Phys. Rev. A. 104, 033107 (2021).
|
“Ultrafast creation of overlapping Rydberg electrons in an atomic BEC and Mott-insulator lattice,”
Michiteru Mizoguchi, Yichi Zhang, Masaya Kunimi, Akira Tanaka, Shuntaro Takeda, Nobuyuki Takei, Vineet Bharti, Kuniaki Koyasu, Tetsuo Kishimoto, Dieter Jaksch, Alexander Glaetzle, Martin Kiffner, Guido Masella, Guido Pupillo, Matthias Weidemüller, and Kenji Ohmori
Phys. Rev. Lett. 124, 253201(2020).
|
“Attosecond Control of Restoration of Electronic Structure Symmetry”,
ChunMei Liu, Jörn Manz, Kenji Ohmori, Christian Sommer, Nobuyuki Takei,
Jean Christophe Tremblay, and Yichi Zhang
Phys. Rev. Lett. 121, 173201 doi:10.1103/PhysRevLett.121.173201 (2018).
|
“Ultrafast Coherent Control of Condensed Matter with Attosecond Precision”,
Hiroyuki Katsuki, Nobuyuki Takei, Christian Sommer, and Kenji Ohmori
Acc. Chem. Res. 51, 1174–1184 (2018).
|
“Direct observation of ultrafast many-body electron dynamics in an ultracold Rydberg gas”,
Nobuyuki Takei, Christian Sommer, Claudiu Genes, Guido Pupillo, Haruka Goto, Kuniaki Koyasu, Hisashi Chiba, Matthias Weidemüller, and Kenji Ohmori
Nature Communications 7, 13449 doi:10.1038/ncomms13449 (2016).
|
“Time-domain Ramsey interferometry with interacting Rydberg atoms”,
Christian Sommer, Guido Pupillo, Nobuyuki Takei, Shuntaro Takeda, Akira Tanaka, Kenji Ohmori, and Claudiu Genes
Phys. Rev. A. 94, 053607 (2016).
|
“Simultaneous manipulation and observation of multiple ro-vibrational eigenstates in solid para-hydrogen”,
Hiroyuki Katsuki and Kenji Ohmori
J. Chem. Phys. 145, 124316 (2016).
|
“Manipulation and visualization of two-dimensional phase distribution of vibrational wave functions in solid parahydrogen crystal”,
Hiroyuki Katsuki, Kenzo Ohmori, Toru Horie, Hisao Yanagi, and Kenji Ohmori,
Phys. Rev. B. 92, 094511 (2015).
|
“Quantum Superrotor”,
Kenji Ohmori
Physics 7, 29 (2014).
|
“Optically Engineered Quantum States in Ultrafast and Ultracold Systems”,
Kenji Ohmori
Found. Phys. 44, 813-818 (2014).
|
“Theoretical/numerical study on strong-laser-induced interference in the B state of I2”,
Y. Ohtsuki, H. Goto, H. Katsuki, and K. Ohmori
Phys. Chem. Chem. Phys. 16, 5689-5697 (2014)
|
“All-Optical Control and Visualization of Ultrafast Two-Dimensional Atomic Motions in a Single Crystal of Bismuth”,
H. Katsuki, J. C. Delagnes, K. Hosaka, K. Ishikawa, H. Chiba, E. S. Zijlstra, M. E. Garcia, H. Takahashi, K. Watanabe, M. Kitajima, Y. Matsumoto, K. G. Nakamura, and K. Ohmori
Nature Communications 4, 2801-1 – 2801-7 (2013).
|
“Optically engineered quantum interference of delocalized wavefunctions in a bulk solid : The example of solid para-hydrogen”,
Hiroyuki Katsuki, Yosuke Kayanuma, and Kenji Ohmori,
Phys. Rev. B. 88, 014507-1- 014507-6(2013).
|
“Wavepacket interferometry for nuclear densities and flux densities”,
Timm Bredtmann, Hiroyuki Katsuki, Jörn Manz, Kenji Ohmori, and Christian Stemmle,
Molecular Physics, 111, 1691-1696 (2013). (invited paper)
|
“Optical manipulation of coherent phonons in superconducting YBa2Cu3O7-d thin films”,
Yasuaki Okano, Hiroyuki Katsuki, Yoshihiro Nakagawa, Hiroshi Takahashi, Kazutaka G. Nakamura and Kenji Ohmori,
Faraday Discuss., 153, 375–382 (2011). (invited paper)
|
“Strong-Laser-Induced Quantum Interference”,
Haruka Goto, Hiroyuki Katsuki, Heide Ibrahim, Hisashi Chiba, and Kenji Ohmori,
Nature Physics, 7, 383–385 (2011).
Highlighted by “News and Views” in Nature Physics. Nature Physics 7, 373–374 (2011).
Highlighted by “Research Highlights” in Nature Photonics. Nature Photonics 5, 382–383 (2011).
|
“Optical modification of the vibrational distribution of the iodine molecule”,
H. Goto, H. Katsuki, and K. Ohmori,
Chem. Phys. Lett. 493, 170-172 (2010).
|
“Wave packet interferometry with attosecond precision and picometric structure”,
H. Katsuki, H. Chiba, C. Meier, B. Girard, and K. Ohmori,
Phys. Chem. Chem. Phys. 12, 5189-5198 (2010).
|
“Ultrafast Fourier transform with a femtosecond-laser-driven molecule”,
K. Hosaka, H. Shimada, H. Chiba, H. Katsuki, Y. Teranishi, Y. Ohtsuki, and K. Ohmori,
Phys. Rev. Lett. 104, 180501-1-180501-4 (2010).
|
“Ultrafast Fourier transform with a femtosecond-laser-driven molecule”,
K. Hosaka, H. Shimada, H. Chiba, H. Katsuki, Y. Teranishi, Y. Ohtsuki, and K. Ohmori,
Phys. Rev. Lett. 104, 180501-1-180501-4 (2010).
Selected for “Editors’ Suggestions” in PRL.
Covered by “Viewpoints” in Physics; Physics 3, 38 (2010).
Covered by “Research Highlights” in Nature; Nature 465, 138-139 (2010).
|
“Optical control and mode selective excitation of coherent phonons in YBa2Cu3O7-d”,
H. Takahashi, K. Kato, H. Nakano, M. Kitajima, K. Ohmori, and K. G. Nakamura,
Solid State Commun. 149, 1955-1957 (2009).
|
“Actively tailored spatiotemporal images of quantum interference on the picometer and femtosecond scales”,
H. Katsuki, H. Chiba, C. Meier, B. Girard, and K. Ohmori,
Phys. Rev. Lett. 102, 103602-1—103602-4 (2009).
|
“Wave-packet and coherent control dynamics”,
Kenji Ohmori,
Annu. Rev. Phys. Chem. 60, 487-511 (2009).
|
“Development of ultrahigh-precision coherent control and its applications”,
Kenji Ohmori,
Proc. Jpn. Acad., Ser. B 84, 167-175 (2008).
|
“READ and WRITE amplitude and phase information by using high-precision molecular wave-packet interferometry”,
H. Katsuki, K. Hosaka, H. Chiba, and K. Ohmori,
Phys. Rev. A 76, 013403-1—013403-13 (2007).
|
“Visualizing picometric quantum ripples of ultrafast wave-packet interference”,
H. Katsuki, H. Chiba, B. Girard, C. Meier, and K. Ohmori,
Science 311, 1589-1592 (2006).
|
“Real-time observation of phase-controlled molecular wave-packet interference”,
K. Ohmori, H. Katsuki, H. Chiba, M. Honda, Y. Hagihara, K. Fujiwara, Y. Sato, and K. Ueda,
Phys. Rev. Lett. 96, 093002-1-093002-4 (2006).
|
“Implementation of quantum gate operations in molecules with weak laser fields”,
Y. Teranishi, Y. Ohtsuki, K. Hosaka, H. Chiba, H. Katsuki, and K. Ohmori,
J. Chem. Phys. 124, 114110-1—114110-9 (2006).
|
“High precision molecular wave-packet interferometry with Hg-Ar dimmers”,
Kenji Ohmori, Yukinori Sato, Evgueni E. Nikitin, and Stuart A. Rice,
Phys. Rev. Lett. 91, 243003-1-243003-4 (2003).
|
“Energy dependence of the intramultiplet mixing cross section in Hg–N2 collisions: conical intersection mechanism, indication at tunneling and interference”,
E.I.Dashevskaya, E.E.Nikitin, K.Ohmori, M.Okunishi, I.Oref, and Y.Sato, Phys. Chem. Chem. Phys. 5, 1198 (2003).
|
“Development of attosecond optical-phase manipulation for the wave-packet engineering”,
K.Ohmori, M.Nakamura, H.Chiba, K.Amano, M.Okunishi, and Y.Sato, J. Photochemistry & Photobiology A: Chemistry 145, 17-21 (2001).
|
“Double-pulse manipulation of vibrational wave packets in HgAr van der Waals complex”,
Y.Sato, H.Chiba, M.Nakamura, and K.Ohmori, in Laser Control and Manipulation of Molecules, edited by R.J.Gordon, A.Bandrauk, and Y.Fujimura (ACS Books, 2001), pp. 155-170.
|
“Spectroscopy of quasimolecular optical transitions: Ca(4s2 1S0 – 4s4p 1P, 4s3d 1D2)-He. The influence of radiation width”,
E.Bichoutskaia, A.Devdariani, K.Ohmori, O.Misaki, K.Ueda, and Y.Sato, J. Phys. B: At. Mol. Opt. Phys. 34, 2301-2312 (2001).
|
“Femtosecond real-time probing of the ultrafast energy dissipation in the Hg(63P1)-CO van der Waals interaction”,
K.Ohmori, K.Amano, H.Chiba, M.Okunishi, and Y.Sato, J. Chem. Phys. 113, 461-464 (2000). (in Communications)
|
“A high-resolution angle-resolved electron spectroscopy study of the 5dnp Rydberg series in Ba”,
K.Ohmori, H.Chiba, K.Amano, K.Ueda, Y.Sato, J.B.West, K.J.Ross, and M.Aymar, J. Phys. B: At. Mol. Opt. Phys. 32, 5223-5235 (1999).
|
“Far-wing excitation study on the transition regions of the metastable mercury atom collisions: Hg(63P2) + N2 and CO”,
K.Ohmori, T.Kurosawa, H.Chiba, M.Okunishi, Y.Sato, A.Z.Devdariani, and E.E.Nikitin, Chem. Phys. Lett. 315, 411-415 (1999).
|
“Collision-induced fine-structure transitions of Hg (63P163P0) with N2 and CO. 1. Initial orbital alignment effects”,
M.Okunishi, J.Hashimoto, H.Chiba, K.Ohmori, K.Ueda, and Y.Sato, J. Phys. Chem. 103, 1734-1741 (1999).
|
“Collision-induced fine-structure transitions of Hg (63P163P0) with N2 and CO. 2. Translational energy dependence”,
M.Okunishi, J.Hashimoto, H.Chiba, K.Ohmori, K.Ueda, and Y.Sato, J. Phys. Chem. 103, 1742-1747 (1999).
|
“Auger electron spectra of CF3CN, CF3Cl, CF2Cl2, and CFCl3”,
Y.Shimizu, K.Ueda, H.Chiba, M.Okunishi, K.Ohmori, Y.Sato, H.Suzuki, T.Ibuki, and K.Okada, Chem. Phys. 244, 439-448 (1999).
|
“Far-wing excitation studies on the quasimolecular transitions in the Hgrare-gas, simple-molecule half-collisions”,
Kenji Ohmori, in Spectral Line Shapes, Vol. 10, edited by R. Herman (AIP Press, 1999), pp.352-363.
|
“Ultrafast pump/probe approach to atom-molecule half-collisions”,
Kenji Ohmori, in LASERS ’98, edited by V.J.Corcoran and T.A.Goldman (STS Press, McLean VA, 1999), pp.106-115.
|
“c←X laser excitation spectrum of the Hg-Ar vdW complex”,
K. Amano, K. Ohmori, Y. Kurosawa, H. Chiba, M. Okunishi, K. Ueda, Y. Sato, A. Z. Devdariani, and E. E. Nikitin, J. Chem. Phys. 108, 8110-8113 (1998).
|
“Collision induced absorption in mercuryrare-gas collisions”,
T.Kurosawa, K.Ohmori, H.Chiba, M.Okunishi, K.Ueda, Y.Sato, A.Z.Devdariani, and E.E.Nikitin, J. Chem. Phys. 108, 8101-8109 (1998).
|
“Apparatus for studying decay and dissociation of core-excited molecules”,
Y.Shimizu, K.Nagao, K.Ueda, M.Takahashi, H.Chiba, S.Yanagida, M.Okunishi, K.Ohmori, Y.Sato, T.Hayaishi, and K.J.Ross, J. Electr. Spectrosc. Relat. Phenom. 88-91, 1031-1036 (1998).
|
“Far-wing excitation studies on the transit regions in slow atomic collisions”,
K.Ohmori and Y.Sato, in Photonic, Electronic and Atomic Collisions, edited by F. Aumayr and HP. Winter (World Scientific, 1998), pp.593-602.
|
“Absolute photoionization cross sections for the Ba ground state in the autoionization region. I. 238-218nm”,
K. Maeda, M. Aymar, K. Ueda, H. Chiba, K. Ohmori, Y. Sato, J. B. West, K. J. Ross, and K. Ito, J. Phys. B: At. Mol. Opt. Phys. 30, 3159-3171 (1997).
|
“Angle-resolved photoelectron and photoion study on the shape resonance in the B 1s ionization region of BF3”,
Y.Shimizu, K.Ueda, H.Chiba, K.Ohmori, M.Okunishi, Y.Sato, and T.Hayaishi, J. Chem. Phys. 107, 2415-2418 (1997).
|
“Symmetries and dissociation dynamics of F 1s core-excited states of BF3”,
Y.Shimizu, K.Ueda, H.Chiba, M.Okunishi, K.Ohmori, J.B.West, Y.Sato, and T.Hayaishi, J. Chem. Phys. 107, 2419-2423 (1997).
|
“Correlation between core-hole polarization and localized bond rupture from anisotropy in the photofragmentation of F 1s excited SF6”,
K.Ueda, Y.Shimizu, K.Nagao, H.Chiba, M.Okunishi, K.Ohmori, J.B.West, Y.Sato, T.Hayaishi, H.Nakamatsu, and T.Mukoyama, Phys. Rev. Lett. 79, 3371-3374 (1997).
|
“Far-wing excitation study of the reactions in the Hg-H2 collisional quasimolecules. I. Transit-state selectivity in HgH formation and three-body dissociation”,
K.Ohmori, T.Takahashi, H.Chiba, K.Saito, T.Nakamura, M.Okunishi, K.Ueda, and Y.Sato, J. Chem. Phys. 105, 7464-7473 (1996).
|
“Far-wing excitation study of the reactions in the Hg-H2 collisional quasimolecules. II. Rovibrational distributions of HgH, HgD (X2+) formed from Hg-H2, D2, HD”,
K.Ohmori, T.Takahashi, H.Chiba, K.Saito, T.Nakamura, M.Okunishi, K.Ueda, and Y.Sato, J. Chem. Phys. 105, 7474-7479 (1996).
|
“Far-wing excitation spectra of the Hg 6s6p3P0-6s7s3S1 inter-excited-state transitions broadened by Ar and Ne”,
K.Ohmori, K.Amano, M.Okunishi, H.Chiba, K.Ueda, and Y.Sato, Chem. Lett. 765-766 (1996).
|
“Continuum absorption spectra in far wings of Hg 1S03P1 resonance line broadened by Ar”,
Y.Sato, T.Nakamura, M.Okunishi, K.Ohmori, H.Chiba, and K.Ueda, Phys. Rev. A 53, 867-873 (1996).
|
“Dissociation dynamics of B 1s core-excited BF3 probed by energy-selected electron energy-selected ion coincidence and angle-resolved ion spectroscopy”,
K.Ueda, K.Ohmori, M.Okunishi, H.Chiba, Y.Shimizu, Y.Sato, T.Hayaishi, E.Shigemasa, and A.Yagishita, J. Elec. Spec. Rel. Phenom. 79, 411-414 (1996).
|
“C 1s and F 1s photoabsorption and subsequent electronic decay of CH4, CH3F, CH2F2, CHF3, and CF4”,
K.Ueda, Y.Shimizu, H.Chiba, M.Okunishi, K.Ohmori, Y.Sato, E.Shigemasa, and N.Kosugi, J. Elec. Spec. Rel. Phenom. 79, 441-444 (1996).
|
“Far-wing excitation study on the transit region of Hg 3P13P0 intramultiplet process in collisions with N2 and CO”,
K.Ohmori, T.Kurosawa, H.Chiba, M.Okunishi, K.Ueda, Y.Sato, and E.E.Nikitin, J. Chem. Phys. 102, 7341-7350 (1995).
|
“Rydberg-valence mixing in the C 1s excited states of CH4 probed by electron spectroscopy”,
K.Ueda, M.Okunishi, H.Chiba, Y.Shimizu, K.Ohmori, Y.Sato, E.Shigemasa, and N.Kosugi, Chem. Phys. Lett. 236, 311-317 (1995).
|
“Direct observation of correlation between electron emission and fragmentation into ions following B 1s excitation of the BF3 molecule”,
K.Ueda, K.Ohmori, M.Okunishi, H.Chiba, Y.Shimizu, Y.Sato, T.Hayaishi, E.Shigemasa, and A.Yagishita, Phys. Rev. A 52, R1815-R1818 (1995).
|
“Rydberg and valence states in the C 1s photoabsorption and resonance Auger spectra of CH3F”,
N.Kosugi, K.Ueda, Y.Shimizu, H.Chiba, M.Okunishi, K.Ohmori, Y.Sato, and E.Shigemasa, Chem. Phys. Lett. 246, 475-480 (1995).
|
“Far-wing excitation study on the fine-structure transition of Hg(3P13P0) in collisions with N2”,
K.Ohmori, T.Kurosawa, H.Chiba, M.Okunishi, and Y.Sato, J. Chem. Phys. 100, 5381-5383 (1994). (in Communications)
|
“Blue satellite structure of the Ba resonance line broadened by rare gases”,
T. Maeyama, H. Ito, H.Chiba, K.Ohmori, K. Ueda, and Y.Sato, J. Chem. Phys. 97, 9492-9493 (1992).
|
“Pressure dependence of the rate constant for the reaction: CH3O+NO”,
K.Ohmori, K.Yamasaki, and H.Matsui, Bull. Chem. Soc. Jpn. 66, 51-56 (1993).
|
“Reaction rates of atomic oxygen(3P) with a series of alkanes at high temperatures”,
A.Miyoshi, K.Ohmori, and H.Matsui, in Turbulence and molecular processes in combustion, edited by T.Takeno (Elsevier, 1993), pp. 85-99.
|
“Reaction rates of atomic oxygen with straight chain alkanes and fluoro-methanes at high temperatures”,
A.Miyoshi, K.Ohmori, K.Tsuchiya, and H.Matsui, Chem. Phys. Lett. 204, 241-247 (1993).
|
“A flash photolysis study of CH4-O2 mixture behind shock waves”,
K.Ohmori, M.Yoshimura, M.Koshi, and H.Matsui, Bull. Chem. Soc. Jpn. 65, 1317-1322 (1992).
|
“Examination of the chain branching steps in oxidation of CH4 and H2S via excimer laser photolysis in shock waves”,
M.Yoshimura, K.Ohmori, K.Kamiya, M.Koshi, and H.Matsui, in Shock Waves, K. Takayama, Ed. (Springer-Verlag, Berlin, 1992), vol. II, pp. 887-890.
|
“Studies on the reaction of acetaldehyde and acetyl radicals with atomic hydrogen”,
K.Ohmori, A.Miyoshi, and H.Matsui, J. Phys. Chem. 94, 3253-3255 (1990).
|
|
K. OHMORI, ” Ultrafast quantum simulation and quantum computing with ultracold atom arrays”, MIT-Harvard Center for Ultracold Atoms (CUA) Seminar, Harvard University, Cambridge, USA, 7 February 2023.
|
|
K. OHMORI, ” Ultrafast quantum simulation and quantum computing with ultracold atom arrays”, The Chicago Quantum Exchange(CQE) Seminar, The University of Chicago, Chicago, USA, 2 February 2023.
|
|
K. OHMORI, “Ultrafast quantum computer/simulator with attosecond precision”, The 4th International Symposium on Quantum Physics and Quantum Information Sciences, Beijing Academy of Quantum Information Sciences, Beijing, China, Online, 30 November 2022.
|
|
K. OHMORI, “Ultrafast quantum computer/simulator operating at the single-atom level”, Virtual Humboldt Colloquium “Top Global Research” and the Humboldt Network: New Frontiers of German-Japanese Scientific Cooperation, Alexander von Humboldt Foundation, Germany, Online, 18 November 2022.
|
|
K. OHMORI, “Ultrafast and ultracold quantum simulator/computer with attosecond precision”, ColdQuanta, Inc., Boulder, USA, Hybrid, 27 July 2022.
|
|
K. OHMORI, “Ultrafast and ultracold quantum simulator/computer with attosecond precision”, Special Summer 2022 Quantum Seminar Series, CUbit Quantum Initiative, University of Colorado Boulder and JILA/NIST, Boulder, USA, Hybrid, 26 July 2022.
|
|
K. OHMORI, “Moonshot proposal: Large-scale and high-coherence fault-tolerant quantum computer with dynamical atom arrays”, ColdQuanta, Inc., Boulder, USA, Hybrid, 25 July 2022.
|
|
K. OHMORI,”Ultrafast and ultracold quantum simulator/computer with attosecond precision”, The 4th Asia-Pacific Workshop on Trapped Quantum Systems(APTQS 2022) , 22 April 2022 (Online).
|
|
K. OHMORI,”Ultrafast and ultracold quantum simulator/computer with attosecond precision”, Quantum Simulations and Computations with Cold Atoms-2022 (QSCCA 2021) , 26 January 2022 (Online).
|
|
K. OHMORI (Invited Talk / Panel Discussion), “Japan’s quantum-technology testbeds,” The International Symposium on Quantum Science, US DOE Office of Science (SC) Workshop on the International Quantum Computing Testbeds, Quantum Computing Testbeds Stakeholder Workshop, US DOE Office of Science (SC), USA, 18 December 2021 (Online).
|
|
K. OHMORI (Invited Talk / Panel Discussion), “Quantum computers and simulators; the present status and future perspectives,” JACS in session with JACS Au and ACS Phys Chem Au for the theme of “Quantum Computing, Data Science, and Computation Evolution for Chemistry and Energy.”, American Chemical Society, USA, 14 December 2021 (Online). (Postponed to 2022 due to various reasons of the organizer, American Chemical Society JACS)
|
|
K. OHMORI, “Ultrafast and ultracold quantum simulator/computer with attosecond precision”, the International Symposium on Quantum Science, Technology and Innovation: QUANTUM INNOVATION 2021, 7-9 December 2021 (Online)
|
|
K. OHMORI, “Ultrafast and ultracold quantum simulator with attosecond precision”, The 5th International Workshop on Rydberg Atoms andMolecules, 28-31 Octorber 2021(Online)
|
|
K. OHMORI, “Ultrafast and Ultracold Quantum Simulator with Attosecond Precision”, IAS Center for Quantum Technologies Inaugural Workshop, 26 August 2021 (Online).
|
|
K. OHMORI, “Ultrafast and ultracold quantum simulator with attosecond precision,” The 15th Femtochemistry Conference (FEMTO 15), Berlin, Germany, 25-30 July 2021.(Postponed to 2023 due to Covid-19 pandemic)
|
|
K. OHMORI, “Ultrafast and ultracold quantum simulator with attosecond precision”, the U.S.-Japan Quantum Cooperation Workshop(Hudson Institute, USA / Cabinet Office, Japan), 1 July 2021 (Online).
|
|
K. OHMORI, “Ultrafast and ultracold quantum simulator with attosecond precision”, DAMOP 2021 (52nd Annual Meeting of the American Physical Society’s Division of Atomic, Molecular and Optical Physics), 31 May-4 June 2021 (Online).
|
|
K. OHMORI, “Ultrafast and ultracold quantum simulator with attosecond precision”, EU FET Project COPAC Symposium “Parallel Computing Quantum Devices”, 23-25 March 2021 (Online).
|
|
K. OHMORI, “Ultrafast quantum simulator with attosecond precision at ultracold temperatures”, Fundamental Sciences and Quantum Technologies using Atomic Systems (FSQT 2020)organized by Atomic, Molecular and Optical Physics Division Physical Research Laboratory, supported by SciRox, Science Club, GNDU, Amritsar, Punjab, India, 29 September, 2020 (Online).
|
|
K. OHMORI, “Ultrafast quantum simulator with attosecond precision at ultracold temperatures”, India-Japan webinar on quantum technologies organized by the Embassy of India, Tokyo, supported by the governments of India and Japan, 28 July 2020 (Online).
|
|
K. OHMORI, “Ultrafast many-body electron dynamics in an ultracold atomic BEC and Mott insulator lattice”, “EU-Japan bilateral meeting on Quantum Science” of “EU-USA-Japan International Symposium on Quantum Technology” and “Topical Conference on Quantum Computing 2019”, Kyoto Brighton Hotel, Kyoto, December 16-18, 2019.
|
|
K. OHMORI,”Ultrafast many-body electron dynamics in an ultracold atomic BEC and Mott insulator lattice”, “Annual Conference Series title: Frontiers in Synthetic Quantum Systems, 2019 Focus: Quantum Simulations in Optical Lattices and Beyond”, Tianping Hotel, Shanghai, China, December 14-15, 2019.
|
|
K. OHMORI, “Ultrafast many-body electron dynamics in an ultracold atomic BEC and Mott insulator lattice”, the Conference “Quantum Computing in Near Term”, Universität Wien, wien, Austria, October 21, 2019.
|
|
K. OHMORI, “International trends of quantum simulation and its future challenges”, JST CRDS, JST Tokyo Headquarters, Tokyo,Septembei 22, 2019.
|
|
K. OHMORI, “Ultrafast many-body electron dynamics in a strongly correlated ultracold Rydberg gas”, The 14th Femtochemistry Conference, Jin Jiang Hotel, Shanghai, China August 1, 2019.
|
|
K. OHMORI, “Ultrafast many-body electron dynamics in a strongly correlated ultracold Rydberg gas”, P&A AMO Seminar, Rice University, Houston, USA July 1, 2019.
|
|
K. OHMORI, “Ultrafast many-body electron dynamics in a strongly correlated ultracold Rydberg gas”, Quantum Dynamics and Spectroscopy in Condensed-Phase Materials and Bio-Systems, Telluride Science Research Center (TSRC), Telluride, USA, June 28, 2019.
|
|
K. OHMORI, “Ultrafast many-body electron dynamics in a strongly correlated ultracold Rydberg gas”, International Symposium: Highly-excited States and Non-covalent Interactions, The University of Manchester, Manchester, UK June 20, 2019.
|
|
K. OHMORI, “Ultrafast many-body electron dynamics in a strongly correlated ultracold Rydberg gas”, the 4th International Workshop on Rydberg Atoms and Molecules, Hangzhou, China, June 7, 2019.
|
|
K. OHMORI, “Ultrafast many-body electron dynamics in a strongly correlated ultracold Rydberg gas”, IAS Workshop, The Hong Kong University of Science and Technology, China, May 7, 2019.
|
|
K. OHMORI, “International trends of quantum simulation and its future challenges”, JST CRDS, JST Tokyo Headquarters, Tokyo, Apri 22, 2019.
|
|
K. OHMORI, “Ultrafast many-body electron dynamics in a strongly correlated ultracold Rydberg gas”, CQOM Colloquium, Center for Quantum Optics and Quantum Matter (CQOM), Aarhus University, Denmark, May 17, 2018.
|
|
K. OHMORI, “Ultrafast Many-Body Electron Dynamics in a Strongly Correlated Ultracold Rydberg Gas”, Max Planck Institute of Quantum Optics, Garching, Germany, March 16, 2018
|
|
K. OHMORI, “Ultrafast Many-Body Electron Dynamics in a Strongly Correlated Ultracold Rydberg Gas”, Joint Quantum Institute, Maryland, USA, March 8, 2018
|
|
K. OHMORI, “Ultrafast Many-Body Electron Dynamics in a Strongly Correlated Ultracold Rydberg Gas”, University of Oxford, Oxford, UK, November 20, 2017.
|
|
K. OHMORI, “Ultrafast Many-Body Electron Dynamics in a Strongly Correlated Ultracold Rydberg Gas”, Max Planck Institute for the Science of Light, Erlangen, Germany, October 5, 2017.
|
|
K. OHMORI, “Ultrafast Many-Body Electron Dynamics in a Strongly Correlated Ultracold Rydberg Gas”, CUA Seminars, MIT-Harvard Center for Ultracold Atoms, Cambridge, USA, September 12, 2017.
|
|
K. OHMORI, “Ultrafast Many-Body Electron Dynamics in a Strongly Correlated Ultracold Rydberg Gas”, Gordon Research Conference on “Quantm Control of Light and Matter”, Mount Holyoke College, South Hadley, MA, USA, August 6-11, 2017.
|
|
K. OHMORI, “Ultrafast Many-Body Electron Dynamics in a Strongly Correlated Ultracold Rydberg Gas”, Institut d’Optique, Palaiseau, France, May 26, 2017.
|
|
K. OHMORI, “Ultrafast Many-Body Electron Dynamics in a Strongly Correlated Ultracold Rydberg Gas”, Les Houches / Telluride Workshop on “Quantum Dynamics and Spectroscopy of Functional Molecular Materials and Biological Photosystems”, Les Houches, France, May 24, 2017.
|
|
K. OHMORI, “Ultrafast Many-Body Electron Dynamics in a Strongly Correlated Ultracold Rydberg Gas”, IQOQI, University of Innsbruck, Austria, May 5, 2017.
|
|
K. OHMORI, “Many-Body Physics: The Holy Grail of Modern Sciences and Technologies”, Invited Lecture, State Key Laboratory of Quantum Optics and Quantum Optic Devices, Shanxi University, China, November 7-11, 2016.
|
|
K. OHMORI, “Addressing Quantum Many-Body Dynamics by Ultrafast Coherent Control with Attosecond Precision”, CQD-IMS Collaborative Meeting “Rydberg Quantum Matter”, Heidelberg, Germany, June 9-10, 2016.
|
|
K. OHMORI, “Many-Body Physics: The Holy Grail of Modern Sciences and Technologies,” 1st International Symposium on Advanced Photonics (ISAP), Hamamatsu, Japan, April 12-14, 2016.
|
|
K. OHMORI, “Direct Observation and Control of Ultrafast Many-Body Electron Dynamics in a Strongly-Correlated Ultracold Rydberg Gas,” OIST Mini Symposium “Rydberg Atoms for Quantum Technologies”, Okinawa, Japan, March 3-5, 2016.
|
|
K. OHMORI, “Addressing Quantum Many-Body Dynamics by Ultrafast Coherent Control with Attosecond Precision”, CQD-IMS Collaborative Meeting “Rydberg Quantum Matter”, Heidelberg, Germany, June 9, 2016.
|
|
K. OHMORI, “Direct Observation of Ultrafast Many-Body Electron Dynamics in a Strongly-Correlated Ultracold Rydberg Gas”, Perspectives in Nano Information Processing: an International Conference and Workshop, Cambridge, UK, December 14-16, 2015.
|
|
K. OHMORI, “Direct Observation of Ultrafast Many-Body Electron Dynamics in a Strongly- Correlated Ultracold Rydberg Gas”, The 12th US-Japan Seminar on Many Body Quantum Systems, Madison, USA, September 20-24, 2015.
|
|
K. OHMORI, “Direct Observation of Ultrafast Quantum Many-Body Dynamics in a Strongly-Correlated Ultracold Rydberg Gas”, The 12th Femtochemistry Conference, Hamburg, Germany, July 12-17, 2015.
|
|
K. OHMORI, “Ultrafast Many-Body Electron Dynamics in a Strongly-Correlated Ultracold Rydberg Gas”, Gordon Research Conference on “Atomic Physics”, Newport, USA, June 14-19, 2015.
|
|
K. OHMORI, “Ultrafast electron dynamics beyond mean-field in a strongly-correlated ultracold Rydberg gas”, Coherence and Control in the Quantum World: Current and Future Trends, Weizmann Institute of Science, Israel, December 15-18, 2014.
|
|
K. OHMORI, “Ultrafast Electron Dynamics Beyond Mean-Field in a Strongly-Correlated Ultracold Rydberg Gas”, SFB Kolloquium, University of Stuttgart, Stuttgart, Germany, October 31, 2014.
|
|
K. OHMORI, “Exploring Quantum-Classical Boundary with Light”, Fujihara Seminar: Real-time Dynamics of Physical Phenomena and Manipulation by External Fields, Tomakomai, Hokkaido, Japan, September 23-27, 2014.
|
|
K. OHMORI,”Ultrafast Many-Body Dynamics in an Ultracold Rydberg Gas”, Ultracold Rydberg Physics Workshop, Granada, Spain, September 10-12, 2014.
|
|
K. OHMORI, “Exploring Quantum-Classical Boundary with Coherent Control”, Coherence and Control in the Quantum World: the Legacy of Moshe Shapiro, University of British Columbia, Canada, August 13-15, 2014.
|
|
K. OHMORI, “Exploring Quantum-Classical Boundary with Light”, Physikalisches Kolloquium of University of Heidelberg (also as Plenary Lecture at 11th Germany-Japan Science Colloquium), Heidelberg, Germany, January 17, 2014.
|
|
K. OHMORI, “Ultrafast Coherent Control of an Ultracold Rydberg Gas”, Networks of Ultra-Cold Rydberg Atoms, Keble College in Oxford, UK, January 9-10, 2014
|
|
K. OHMORI, “Ultrafast Coherent Control of an Ultracold Rydberg Gas”, Laser Science XXIX, (the 29th Annual Meeting of the American Physical Society), Hilton Bonnet Creek, Florida, USA, October 6-10, 2013
|
|
K. OHMORI, “Ultrafast Coherent Control of an Ultracold Rydberg Gas”, Conference on Quantum Information and Quantum Control, Fields Institute, Toronto, Canada, Aug 12- 16, 2013.
|
|
K. OHMORI, “Ultrafast Coherent Control of an Ultracold Rydberg Gas”, Gordon Research Conference on “Quantm Control of Light and Matter”, Mount Holyoke College, South Hadley, MA, USA, July 28 – August 2, 2013.
|
|
K. OHMORI, “Ultrafast Coherent Control of an Ultracold Rydberg Gas”, Quantum Dynamics and Spectroscopy in Condensed-Phase Materials and Bio-Systems, TSRC, Telluride, USA, July 8-12, 2013.
|
|
K. OHMORI, “Spatiotemporal Quantum Engineering with Picometer and Attosecond Precision”, Strasbourg Physique Seminaires, Strasbourg University, Strasbourg, France, May 23, 2013.
|
|
K. OHMORI, “Spatiotemporal Quantum Engineering with Picometer and Attosecond Precision”, Atomic and laser physics seminar series, Department of Physics, University of Oxford, Oxford, UK, May 20, 2013.
|
|
K. OHMORI, “Ultrafast Coherent Control of an Ultracold Rydberg Gas”, The 11th US-Japan Joint Seminar on Quantum Electronics and Laser Spectroscopy (The US-Japan QELS-11) “Ultimate Quantum Systems of Light and Matter- Control and Applications”, Nara, Japan, April 11, 2013.
|
|
K. OHMORI, “Optically Engineered Quantum States in Ultrafast and Ultracold Systems”, 3rd IMS-ENSCP Joint Seminar, IMS, Okazaki, Japan, February 13, 2013.
|
|
K. OHMORI, “Optically Engineered Quantum States in Ultrafast and Ultracold Systems”, KITP Program “Fundamental Science and Applications of Ultra-cold Polar Molecules”, KITP UC Santa Barbara, Santa Barbara, USA, February 5, 2013.
|
|
K. OHMORI, “Optically Engineered Quantum States in Ultrafast and Ultracold Systems”, Physics Colloquium, University of Freiburg, Freiburg, Germany, December 3, 2012.
|
|
K. OHMORI, “Optically Engineered Quantum States in Ultrafast and Ultracold Systems”, ESF Research Conference in Partnership with LFUI on “Cold and Ultracold Molecules”, Universitätszentrum Obergurgl, Austria, November 22, 2012.
|
|
K. OHMORI, “Optically Engineered Quantum States in Ultrafast and Ultracold Systems”, Workshop on “Molecular Functional Dynamics: Fundamental to Life Activity”, IMS, Okazaki, Japan, October 26, 2012.
|
|
K. OHMORI, “Optically Engineered Quantum States in Ultrafast and Ultracold Systems”, International Workshop: “Horizons of Quantum Physics: from Foundations to Quantum-Enabled Technologies”, American Club Taipei, Taipei, Taiwan, October 16, 2012.
|
|
K. OHMORI, “Quantum simulator of quantum/classical boundary”, The ‘240’ Conference, The University of Chicago, Chicago, USA, September 14, 2012.
|
|
K. OHMORI, “Exploring quantum/classical boundary”, The ‘240’ Conference, The University of Chicago, Chicago, USA, September 13, 2012.
|
|
K. OHMORI, “Ultrafast Coherent Control of an Ultracold Rydberg Gas”, Batsheva de Rothschild Seminar on “Laser Control of Chemical Reactions: Toward Deciphering Mechanisms and Understanding the Theoretical and Experimental Limits”, Ruth-Rimmonim Hotel, Safed, Israel, September 3, 2012.
|
|
K. OHMORI, “Spatiotemporal quantum engineering with picometer and attosecond precision”, Special Seminar on “Theoretical Chemistry”, Institut für Chemie und Biochemie, Freie Universitaet Berlin, Berlin, Germany, June 19, 2012.
|
|
K. OHMORI, “Optically Engineered Quantum States in Ultrafast and Ultracold Systems”, International Conference on Superconductivity and Magnetism: ICSM 2012, Artemis Marin Princess Hotel, Kumburgaz-Istanbul, Turkey, May 4, 2012.
|
|
K. OHMORI, “Optically Engineered Quantum States in Ultrafast and Ultracold Systems”, IMS Japan – WIS Workshop, Weizmann Institute of Science, Rehovot, Israel, February 26, 2012.
|
|
K. OHMORI, “Single Molecule can Calculate 1000 Times Faster than Supercomputers”, KAIST Physics Coloquium, Daejon, Korea, February 13, 2012.
|
|
K. OHMORI, “Optically Engineered Quantum States in Ultrafast and Ultracold Systems”, Center for Quantum Dynamics Seminar, Universitaet Heidelberg, Heidelberg, Germany, January 19, 2012.
|
|
K. OHMORI, “Ultrafast Computing with a Femtosecond-Laser-Driven Molecule”, Architecture and Design of “supported” single Molecule Logic Gates and atom circuits, Barcelona, Spain, January 12-13, 2012.
|
|
K. OHMORI, “Single Molecule can Calculate 1000 Times Faster than Supercomputers”, International Symposium on Physics and Applications of Laser Dynamics 2011, Tainan, Taiwan, December 7, 2011.
|
|
K. OHMORI, “Optically Engineered Quantum States in Ultrafast and Ultracold Systems”, Meet APS Fellow Forum, National Tsing Hua University, Hsinchu, Taiwan, December 6, 2011.
|
|
K. OHMORI, “Attosecond Quantum Engineering”, Germany-Japan Colloquium “From the Early Universe to the Evolution of Life”, Heidelberg, Germany, December 1-3, 2011.
|
|
K. OHMORI, “Single Molecule can Calculate 1000 Times Faster than Supercomputers”, Frontier in Molecular Science based on Photo and Material, Paris, France, November 7-8, 2011.
|
|
K. OHMORI, “Ultrafast Computing with a Femtosecond-Laser-Driven Molecule”, International Workshop on Simulation and Manipulation of Quantum Systems for Information Processing (SMQS-IP), Juelich, Germany, October 17-19, 2011.
|
|
K. OHMORI, “Ultrafast Computing with a Femtosecond-Laser-Driven Molecule”, International Workshop “Engineering and Control of Quantum Systems”, Dresden, Germany, October 10-14, 2011.
|
|
K. OHMORI, “Ultrafast Computing with a Femtosecond-Laser-Driven Molecule”, International Workshop on Coherence and Decoherence at Ultracold Temperatures, Institute for Advanced Study of Technische Universitat Munchen in Garching/Munich, Germany, September 6-9, 2011.
|
|
K. OHMORI, “Coherent Control; Present and Future”, Gordon Research Conference on “Quantm Control of Light and Matter,” Mount Holyoke College, South Hadley, MA, USA, July 31 – August 5, 2011.
|
|
K. OHMORI, “Single Molecule Can Calculate 1000 Times Faster than Supercomputers”, Special Seminar at Physics Department of Oxford University, Oxford, UK, July 28, 2011.
|
|
K. OHMORI, “Optical Manipulation of Coherent Phonons in Superconducting YBa2Cu3O7-δ Thin Films”, Faraday Discussion 153: Coherence and Control in Chemistry, Leeds, UK, July 25-27, 2011.
|
|
K. OHMORI, “Single Molecule can Calculate 1000 Times Faster than Supercomputers”, 14th Korea-Japan Joint Symposium on Frontiers of Molecular Science”New Visions for Spectroscopy and Computation: Temporal and Spatial Adventures of Molecular Sciences”, Busan, Korea, July 6-8, 2011.
|
|
K. OHMORI, “Molecular Eigenstate-Based Information Processing”, Lorentz Center Workshop on “Molecular Logic”, Lorentz Center, Leiden, Netherland, May 30 – June 2, 2011.
|
|
Kenji Ohmori, “Ultrafast Fourier Transfrom with a Femtosecond-Laser-Driven Molecule”, Séminaire SYRTE, l’Observatoire de Paris, Paris, France, March 7, 2011.
|
|
Kenji Ohmori, “Ultrafast Fourier Transfrom with a Femtosecond-Laser-Driven Molecule”, Séminaire IPCMS, Université de Strasbourg, Strasbourg, France, March 4, 2011.
|
|
Kenji Ohmori, “Ultrafast Fourier Transfrom with a Femtosecond-Laser-Driven Molecule”, ERATO Macroscopic Quantum Control Conference on Ultracold Atoms and Molecules, Tokyo, Japan, January 25, 2011.
|
|
Kenji Ohmori, “Ultrafast Coherent Control of Ultracold Molecules”, Pacifichem 2010, Honolulu, USA, December 17, 2010.
|
|
Kenji Ohmori, “Simulating Molecular Wave Functions Distorted by Impulsive Electronic Interaction with an Intense Femtosecond Laser Pulse”, Pacifichem 2010, Honolulu, USA, December 16, 2010.
|
|
Kenji Ohmori, “Ultrafast Fourier Transfrom with a Femtosecond-Laser-Driven Molecule”, Chemistry Department Seminar Series of Temple University, Philadelphia, USA, October 21, 2010.
|
|
Kenji Ohmori, “Ultrafast Fourier Transfrom with a Femtosecond-Laser-Driven Molecule”, ASILS6, Peking, China, October 15, 2010.
|
|
Kenji Ohmori, “Coherent Control and the Quantum/Classical Boundary”, Physical Chemistry Colloquium, L u d w i g – M a x i m i l i a n s – U n i v e r s i t ä t M ü n c h e n , Munich, Germany, June 2, 2010.
|
|
Kenji Ohmori, “Ultrafast Fourier Transform with a Femtosecond-Laser Driven Molecule”, 6th International Workshop on Optical Control of Quantum Dynamics: Theory and Experiment, Ringberg Castle, Tegernsee, Germany, May 30 – June 2, 2010.
|
|
Kenji Ohmori, “Spatiotemporal Wave-Packet Engineering with Picometer and Attosecond Precision”, Center for Quantum Dynamics Seminar, U n i v e r s i t ä t Heidelberg , Heidelberg, Germany, May 28, 2010.
|
|
Kenji Ohmori, “Spatiotemporal Wave-Packet Engineering with Picometer and Attosecond Precision”, Molecular Physics Seminars, Fritz-Haber-Institut der Max-Planck-Gesellschaft , Berlin, Germany, May 26, 2010.
|
|
Kenji Ohmori, “Coherent Control and the Quantum/Classical Boundary; From Cold Molecules to Bulk Solids”, International Workshop on Coherence in Ultracold Molecular Physics, Vancouver, Canada, May 20-23, 2010.
|
|
Kenji Ohmori, “Spatiotemporal Coherent Control with Picometer and Attosecon Precision; From cold molecules to bulk solids”, Symposium on “Physics and Chemistry of Coherently Controlled Quantum Systems”, Inuyama, March 18-20, 2010.
|
|
Kenji Ohmori, “Spatiotemporal Coherent Control with Picometer and Attosecon Precision; From cold molecules to bulk solids”, The 69th Okazaki Conference on “New Frontier in Quantum Chemical Dynamics”, Okazaki, Japan, February 21-23, 2010.
|
|
Kenji Ohmori, “Spatiotemporal Coherent Control with Picometer and Attosecon Precision; From cold molecules to bulk solids”, LCLS-PULSE seminar series, Stanford, USA, January 11, 2010.
|
|
Kenji Ohmori, “Spatiotemporal Coherent Control with Picometer and Attosecon Precision; From cold molecules to bulk solids”, Ultrafast X-ray Science Laboratory (UXSL) seminar series, Berkeley, USA, January 8, 2010.
|
|
Kenji Ohmori, “Spatiotemporal Coherent Control with Picometer and Attosecon Precision; From cold molecules to bulk solids”, 40th Winter Colloquium on The Physics of Quantum Electronics, Snowbird, USA, January 3-7, 2010.
|
|
Kenji Ohmori, “Spatiotemporal Coherent Control with Picometer and Attosecond Precision ~ From Laser-Cooled Atoms to Bulk Solid”, The 4th Winter School of Asian CORE Program “New Perspectives in Material, Photo and Theoretical Molecular Sciences”, Seoul, Korea, December 14-15, 2009.
|
|
Kenji Ohmori, “Exploring Quantum/Classical Boundary”, Sokendai Asian Winter School “Molecular Science – Central Role in Multidisciplinary Fields”, Okazaki, Japan, December 1-4, 2009.
|
|
Kenji Ohmori, “Spatiotemporal Coherent Control with Picometer and Attosecond Precision ~ from ultracold atoms to bulk solid”, Oregon Center for Optics Annual Retreat 2009, McMinnville, USA, September 17 – 18, 2009.
|
|
Kenji Ohmori”, Spatiotemporal Coherent Control with Picometer and Attosecond Precision”, MIT–Harvard Center for Ultracold Atoms Special Seminar, Harvard University, Cambridge, USA, July 6, 2009.
|
|
Kenji Ohmori, “Spatiotemporal Coherent Control with Picometer and Attosecond Precision”, Gordon Research Conference on “Atomic Physics”, Tilton, USA, June 28 – July 3, 2009.
|
|
Kenji Ohmori, “Spatiotemporal Coherent Control with Picometer and Attosecond Precisions”, The Center for Advanced Photonics Research Laser Science Seminar Series, Temple University, Philadelphia, USA, June 26, 2009.
|
|
Kenji Ohmori, “Spatiotemporal Coherent Control with Picometer and Attosecond Precisions”, The Third International Conference on the Science and Technology for Advanced Ceramics (STAC-3), Yokohama, Japan, June 16-18, 2009.
|
|
Kenji Ohmori, “Spatiotemporal Coherent Control with Picometer and Attosecond Precisions”, ACS 237th National Meeting, Salt Lake City, USA, March 22-26, 2009.
|
|
Kenji Ohmori, “Quantum Ripples in Molecules; Observation and Control”, Sokendai Asian Winter School “Molecular Sciences on Different Space-Time Scales”, Okazaki, Japan, December 11, 2008.
|
|
Kenji Ohmori, “Ultrafast Coherent Control of Picometric Quantum Ripples in Molecules”, 8th Symposium on Extreme Photonics “Ultrafast Meets Ultracold,” Gamagori, Japan, November 11, 2008.
|
|
Kenji Ohmori, “Visualizing and Controlling Picometric Quantum Ripples in Molecules”, The 6th Asia Pacific Laser Symposium, Nagoya, Japan, January 30, 2008.
|
|
Kenji Ohmori, “Quantum Coherence in Molecules; Observation and Control”, COAST/CORAL Winter School on Advanced Laser Science, Echigo Yuzawa, Japan, January 16, 2008.
|
|
Kenji Ohmori, “Tailoring Picometric Quantum Carpets by Controlling Ultrafast Wave-Packet Interference”, 38th Winter Colloquium on The Physics of Quantum Electronics, Snowbird, USA, January 8, 2008.
|
|
Kenji Ohmori (Invited Speaker), “Visualizing and Controlling Picometric Quantum Ripples in Molecules”, The Brijuni 2007 Conference on Laser Pulse Shaping and Coherent Control of Molecules, Brijuni, Croatia, August 26-31, 2007.
|
|
Kenji Ohmori, “Visualizing and Controlling Picometric Quantum Ripples in Molecules”, Gordon Research Conference on “Quantum Control of Light and Matter”, Newport, USA, August 12-17, 2007.
|
|
Kenji Ohmori, “Visualizing and Controlling Picometric Quantum Ripples in Molecules”, Workshop on Coherent Control of Ultracold Molecular Processes, Vancouver, Canada, August 1-4, 2007.
|
|
Kenji Ohmori, “Visualizing and Controlling Picometric Quantum Ripples in Molecules”, ICPEAC XXV, Freiburg, Germany, July 25-31, 2007.
|
|
Kenji Ohmori, “Visualizing and Controlling Picometric Quantum Ripples in Molecules”, International Symposium on Molecular Science of Ultrafast Electronic Dynamics, Sendai, Japan, May 18-19, 2007.
|
|
Kenji Ohmori, “Visualizing and Controlling Picometric Quantum Ripples in Molecules”, 66th Okazaki Conference “Soft X-Ray Raman Spectroscopy and Related Phenomena”, Okazaki, Japan, August 17-19, 2006.
|
|
Kenji Ohmori, “Visualizing and Controlling Picometric Quantum Ripples in Molecules”, The 1st Canada-Japan SRO-COAST Symposium on Ultrafast Intense Laser Science, Tokyo, Japan, July 7-8, 2006.
|
|
Kenji Ohmori, “Observation and Control of Picometric Quantum Ripples in a Molecule”, 5th International Symposium for Ultrafast Surface Dynamics, Abashiri, Japan, May 21-25, 2006.
|
|
Kenji Ohmori, “Ultrahigh-Precision Coherent Control of Molecular Wave Packets”, Pacifichem 2005, Hawaii, USA, December 15-20, 2005.
|
|
Kenji Ohmori, “Visualizing Picometric Quantum Ripples of Ultrafast Wave-Packet Interference”, International Symposium on Ultrafast Intense Laser Science 4, Hawaii, USA, December 10-14, 2005.
|
|
Kenji Ohmori, “Phase Sensitive Memory in Molecular Wave Packets; READ and WRITE”, 11th Japan-Korea Joint Symposium on Frontiers in Molecular Science, Okazaki, Japan, March 15-17, 2005.
|
|
Kenji Ohmori, “Phase Sensitive Memory in Molecular Wave Packets; READ and WRITE”, International Seminar on Atomic Processes in Intense Laser Fields and Related Many-Body Phenomena, Hayama, Japan, January 20-23, 2005.
|
|
Kenji Ohmori, “High-Precision Coherent Control of Molecules”, The Fourth Asian Photochemistry Conference, Taipei, Taiwan, January 5-10, 2005.
|
|
Kenji Ohmori, “High-Precision Molecular Wave-Packet Interferometry”, The 24th Physical Chemistry Colloquium “Ultrafast Phenomena – Pico to Atto seconds -“, Sendai (Japan), August 2-3, 2004.
|
|
Kenji Ohmori, “Sub-10 Attosecond Manipulation of Quantum Phases”, The 5th Pacific Rim Conference on Lasers and Electro-Optics: CLEO/Pacific Rim 2003, Taipei, Taiwan, December 15-19, 2003.
|
|
Kenji Ohmori, “Molecular wave-packet interferometry with sub-10 attoseconds quantum phase manipulation”, Japan-Korea Joint Seminar on Frontiers of Advanced Molecular Science: Spectroscopy of Ultra-Resolution in Time, Space and Energy, Wako, Japan, November 19-21, 2003.
|
|
Kenji Ohmori, “Single Molecule Quantum Register”, International Symposium on Ultrafast Intense Laser Science 2: propagation and interaction, Quebec, Canada, September 27-29, 2003.
|
|
Kenji Ohmori, “Sub-10 Attosecond Manipulation of Quantum Phases”, XX International Symposium on Molecular Beams, Lisbon, Portugal, June 8-13, 2003.
|
|
Kenji Ohmori, “Sub-10 Attosecond Manipulation of Quantum Phases”, Fifth Asian International Seminar on Atomic and Molecular Physics: AISAMP 5, Nara, Japan, October 1-5, 2002.
|
|
Kenji Ohmori, “Single Molecule Quantum Memory”, International Symposium on Advanced Laser Manipulation of Molecular Systems, Sendai, Japan, September 6, 2002.
|
|
Kenji Ohmori, “Attosecond wavepacket engineering”, The 6th East Asian Workshop on Chemical Reactions, Seoul, Korea, March 20-24, 2002.
|
|
Kenji Ohmori, “Femtosecond spectroscopy of molecular dynamics and attosecond wave packet engineering”, The 5th East Asian Workshop on Chemical Reactions, Sendai, Japan, March 23-25, 2001.
|
|
Kenji Ohmori, “Femtosecond spectroscopy of molecular dynamics and attosecond wave packet engineering”, The 4th NIMC International Symposium on Photoreaction Control and Photofunctional Materials (PCPM2001), Tsukuba, Japan, March 14-16, 2001.
|
|
Kenji Ohmori, “Optical Collision approach to the ultrafast dynamics in the transition regions”, The 4th East Asian Workshop on Chemical Reactions, Kaohsiung, Taiwan, March 14-17, 2000.
|
|
Kenji Ohmori, “Optical Collision to Control the Transition-Region Dynamics”, Japan-U.S. Seminar “Quantum Control of Chemical Reaction Dynamics”, Honolulu, USA, December 12-15, 1999.
|
|
Kenji Ohmori, “Optical Collision to Open the Doorway to the Transition State”, International Workshop on Stereo Dynamics, Sendai, Japan, July 21, 1999.
|
|
Kenji Ohmori, “Optical Collision to Open the Doorway to the Transition State”, The 3rd East Asian Workshop on Chemical Reactions, Kyoto, Japan, March 16-19, 1999.
|
|
Kenji Ohmori, “Ultrafast Pump/Probe Approach to Atom-Molecule Half Collisions”, The 21st International Conference on Lasers & Applications: LASERS ’98, Tucson AZ, USA, December 7-11, 1998.
|
|
Kenji Ohmori, “Far-Wing Excitation Studies on the Quasimolecular Transitions in the HgRare-Gas, Simple-Molecule Half-Collisions”, 14th International Conference on Spectral Line Shapes, State College PA, USA, June 22-26, 1998.
|
|
Kenji Ohmori, “Far-Wing Excitation Studies on the Transit Regions in Slow Atomic Collisions”, XXth International Conference on the Physics of Electronic and Atomic Collisions, Vienna, Austria, July 23-29, 1997.
|
|
Kenji Ohmori, “Photoionisation of Ba Atoms Using a UV Laser Source”, International Workshop on Photoionisation ’97, Chester, England, July 16-21, 1997.
|